
【連載】#2 twigl.app で始める GLSL クリエイティブコーディング! スクリーン座標正規化を理解する
最初はよくわからないアイツ
twigl.app で始める GLSL クリエイティブコーディング、第二回となる今回のテーマは「よく見かけるスクリーン座標正規化を理解する」です。
twigl.app のように、GLSL を使ってクリエイティブコーディングを行うことができるプラットフォームは実は結構たくさんあるのですが、そのなかでも老舗と言えば GLSL Sandbox と Shadertoy です。
両者は微妙に環境が異なるのですが、GLSL のみを利用してグラフィックスを生成することができるプラットフォーム、という点は共通しています。今回はそれらの GLSL クリエイティブコーディング界隈で見かけることが多い割に、最初は何をやっているのかよくわからない「スクリーン座標の正規化」における定番処理について解説したいと思います。
twigl.app のモードの違い
GLSL でクリエイティブコーディングを行う、とひとくちに言っても、実際にはそのバリエーションは無数にあります。
なにかしらのサードパーティツールを使う場合を筆頭に、自家製のツールを使う場合、あるいは twigl.app などのウェブサービスを使う場合など、それぞれのプラットフォームごとに想定される条件は様々です。とは言え、ここではあくまでも twigl.app のようなウェブをプラットフォームとする場合を前提にした話をしていきます。
twigl.app は、実行環境としては GLSL Sandbox のグラフィックス処理と、Shadertoy の Sound Shader に対する互換性があります。そのような理由から、ここでは海外も含め最もよく知られている(かつ利用されてきた) GLSL Sandbox 仕様のグラフィックス描画について説明していくことにしましょう。ここで説明する内容をしっかり理解しておけば、twigl.app の classic モードや GLSL Sandbox 上で任意のコードを書くことができるようになります。
そもそもの話になっちゃいますが、twigl.app には「モード」という概念があります。
画面の右側にある Regulation の項目から、任意のモードを選択することができるようになっており、種類としては classic, geek, geeker の三種類と、それぞれに対するサブモードがあります。
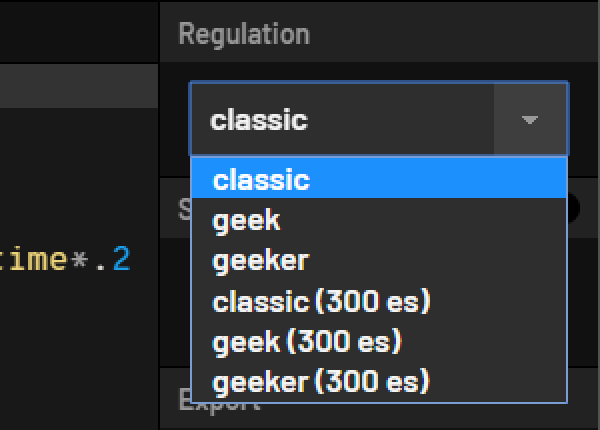
この記事の執筆時で6種類のモードが存在。
(300 es) の記載があるサブモードは、実行される GLSL のバージョンを変更するモードとなっており、これについてはもう少し GLSL 自体の理解が深まってから詳細を理解すれば十分でしょう。
いずれは説明することになるかもしれませんが、ここではまず、通常の classic モードを選択している場合で考えていきましょう。
classic モードは、その語感のとおり「クラシカルで昔ながらの記述スタイル」で GLSL を記述します。前回の記事で触れたようないくつかの uniform 変数を持ち、実行環境としては WebGL 1.0 を利用します。このモードはほぼ完全な GLSL Sandbox 互換となります。
スクリーン座標の正規化
さて、そんな classic モードを選択した際にデフォルトで twigl.app 上に表示されるシェーダは次のようになっています。
precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;
void main(){vec2 r=resolution,p=(gl_FragCoord.xy*2.-r)/min(r.y,r.x)-mouse;for(int i=0;i<8;++i){p.xy=abs(p)/abs(dot(p,p))-vec2(.9+cos(time*.2)*.4);}gl_FragColor=vec4(p.xxy,1);}
main 関数の中身が若干カオスなことになっていますが、それ以外は、第一回で解説に利用したごくごくシンプルな GLSL のコードとほとんど同じ構造をしています。
あらかじめ記述されている uniform 変数は3つあり、それぞれの意味が以下のとおり。
uniform vec2 resolution; // スクリーンの解像度(ピクセル)
uniform vec2 mouse; // マウスカーソルの位置(0.0 ~ 1.0)
uniform float time; // 経過時間(秒)
GLSL によるグラフィックスが描画されるスクリーンの解像度、マウスカーソルのスクリーン上での位置を 0.0 ~ 1.0 の範囲になるように正規化したもの、あとは単純な経過秒数(1秒経過した時点で 1.0 となる)です。
resolution と mouse が vec2 型になっているのは、これらは XY の2つの要素を持っているからですね。
resolution.x のように記述すれば、スクリーンの横幅がわかる、という具合です。
注意しなければならないのは、GLSL の世界では「スクリーン空間は 左下が原点 である」ということでしょう。
通常、ウィンドウや、そのクライアント領域上での座標の表現って「左上」が原点になっていることが多いですよね。右に行くほど X の要素が大きくなり、下に行くほど Y の要素が大きくなる座標系です。
これに対して GLSL の座標系は左下が原点なので、X については同じですが Y は上下が反転したような座標系になっています。これにはちょっと最初は注意が必要かもしれません。

上記を踏まえた上で、今回まず最初に理解しておきたい「GLSL でよく見るやつ」が、以下のようなコードです。
この手のコードは、GLSL でクリエイティブコーディングを行う系の調べ物をしていると、よく目にするのではないでしょうか。
// パターン1
vec2 p = gl_FragCoord.xy / resolution;
// パターン2
vec2 p = gl_FragCoord.xy / resolution * 2.0 - 1.0;
// パターン3
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / min(resolution.x, reslution.y);
ここで掲載した以外にも、いくつかパターンはあるかなと思いますが、だいたいこれと似たような構造になっているものが多いと思います。上記の3パターンは、いずれも異なる計算結果になりますが、やりたいことの意図は共通していて……
スクリーン空間の座標を正規化する ために、このようなコードを書きます。
どういうことか、ちょっとわかりにくいですかね……
正規化という言葉がね、ちょっと難しいですよね。
もう少し砕けた言い方をすると「そのまま gl_FragCoord を使うとなにかと面倒なので、スクリーン空間を一定の尺度に揃えたい」という感じでしょうか。
たとえば、twigl.app ってウェブブラウザで見られるわけですから、解像度の大きなディスプレイでフルスクリーンで見ているユーザーもいれば、小さくリサイズしたウィンドウで見ているユーザーや、モバイル端末のような物理的に解像度の低いスクリーンで見ているユーザーもいるかもしれないわけですよね。
実行される環境が一定でないとして、自分の作った作品は「絶対にこの解像度で見てください! 仕様なんで!」というふうに不特定多数の人に強制することは不可能です。となると理想的には、どのような解像度でも、ある程度似たような絵が出てほしいと考えるのが普通でしょう。
これを実現するために 解像度に依存せずに常に同じような座標系で動作するように調整する のがスクリーン座標の正規化処理です。
たとえば、先程掲載したいくつかのパターンのうち、最初のパターン1を再度掲載してみます。
// パターン1
vec2 p = gl_FragCoord.xy / resolution;
これをよく見ると、まず最初に vec2 p とあるので、ここでは vec2 型の変数 p を宣言しています。
そこに代入されている値を見てみると、ここでは gl_FragCoord.xy を解像度で割る(除算)処理を行っています。
かなりシンプルな計算ですが、このような「なにかしらの計算を行う場面」では変数の中身に仮の値を設定してしまってから、処理の流れを追いかけてみると何が起こっているのかわかりやすいでしょう。
たとえば「実行されているスクリーンの解像度が 1000 x 500 のサイズ」と仮定してみます。GLSL ではベクトル同士の計算結果はそのまま同じ型のベクトルとして処理されますが、ここではわかりやすさのために、あえて冗長な書き方を使って意味としてはまったく同じ処理を行っている様子を書いてみます。
uniform vec2 resolution; // ここが vec2(1000.0, 500.0) だと仮定する
(中略)
vec2 p = vec2(
gl_FragCoord.x / 1000.0,
gl_FragCoord.y / 500.0
);
当たり前のことではありますが、gl_FragCoord.xy は今まさに処理されようとしているピクセルの座標(0.0 はじまり)なので「最大でも解像度と同じ範囲までしか大きくなり得ない」わけですから、X の場合も Y の場合も、計算結果は絶対に 0.0 以上 ~ 1.0 未満に収まることがわかります。
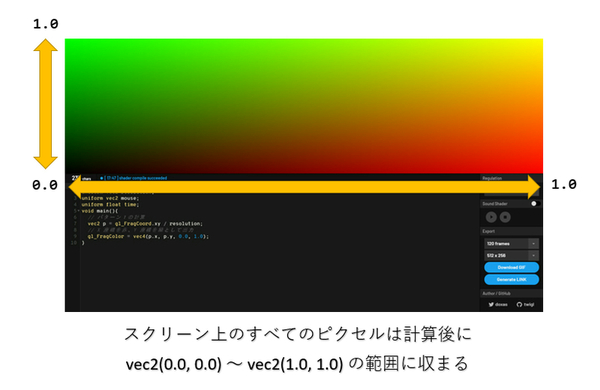
つまり、パターン1のような計算を行ってやり、計算結果である変数 p の値をそのまま出力される色の R と G に出力するようなコードを書いてやると、次のような結果になります。
precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;
void main(){
// パターン1の計算
vec2 p = gl_FragCoord.xy / resolution;
// X 座標を赤、Y 座標を緑として出力
gl_FragColor = vec4(p.x, p.y, 0.0, 1.0);
}
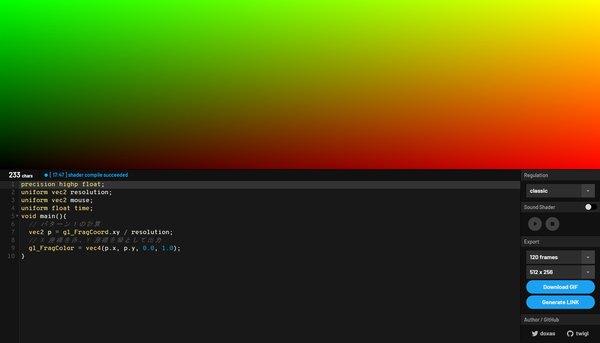
このように、XY 座標が常に 0.0 ~ 1.0 の範囲である、とだけ考えられる状態を作ってしまえば、あとは実行環境の解像度が大きいか小さいかなどは気にする必要がなくなります。
値の大小ではなく、0.0 ~ 1.0 の範囲という、一定の割合いだけで考えられる状態って言ったらいいですかね……
GLSL で処理を書くときは、こういう「スケールによらない統一された規格で話をしたい場面」というのがよく出てくるので、まあ大抵の場合は、スクリーンの座標系を正規化するような処理を行うことが多くなっています。
その他のスクリーン座標正規化パターン
先程掲載した、その他のスクリーン座標系の正規化の例も、実際にどのような処理が行われるているのか見てみましょう。
まずは、パターン2のケース。
// パターン2
vec2 p = gl_FragCoord.xy / resolution * 2.0 - 1.0;
GLSL に限らず、一般的にプログラミング言語では「加減算と乗算・除算」であれば、優先順位は乗算・除算のほうが高くなります。
つまりこのパターン2を先程のパターン1のときのように、解像度が 1000 x 500 だと想定して少し整形してやると……
vec2 p = vec2(
( (gl_FragCoord.x / 1000.0) * 2.0 ) - 1.0,
( (gl_FragCoord.y / 500.0) * 2.0 ) - 1.0
);
こんな感じですかね。
一番内側の括弧で囲まれている (gl_FragCoord.x / 1000.0) の部分がとり得る範囲は 0.0 ~ 1.0 なので、それを2倍すると、とり得る範囲が 0.0 ~ 2.0 となり、そこからさらに 1.0 を減算するので……
最終的に、変数 p に代入される値の範囲は -1.0 ~ 1.0 ということになります。
こいつもパターン1と同じように、計算結果を色の RG 要素に対して出力してみると、以下のようになります。
precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;
void main(){
vec2 p = vec2(
( (gl_FragCoord.x / resolution.x) * 2.0 ) - 1.0,
( (gl_FragCoord.y / resolution.y) * 2.0 ) - 1.0
);
gl_FragColor = vec4(p.x, p.y, 0.0, 1.0);
}
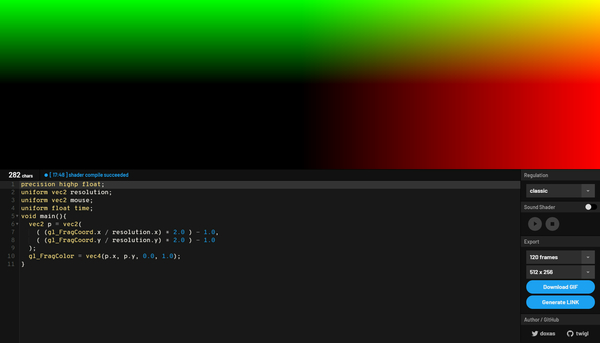
もうここまでくれば、だいたいどんなことが起こっているのか、わかってきたのではないでしょうか。
スクリーン全体の解像度は実行環境によってマチマチなので、統一したフォーマットにするために gl_FragCoord.xy や resolution を使って計算を行っているわけですね。
ちなみに、パターン1のときは画面全体が赤と緑でグラデーションしていましたが、パターン2の場合は黒っぽい領域が左下あたりに生まれています。この黒い領域は、計算結果が負の数値になってしまった場合に、マイナスの色というのは GLSL では存在しないため切り上げられ 0.0 相当として出力されたものです。
最後にダメ押しな感じで、パターン3も見てみましょう。
もともとのコードは、このようなかんじ。ちょっと横に長い……
// パターン3
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / min(resolution.x, reslution.y);
これまでのパターン1やパターン2とは異なり min という関数を使って処理を行っています。
GLSL の min は、JavaScript なら Math.min として実装されている一般的な算術系の関数で、その名前が示すとおり 与えられた引数のうち、小さいほうだけを返す という挙動です。つまり比較したい値が2つあるときに、小さいほうだけを取り出したい(小さいほうを判定したい)場合に役立ちます。
これも、今まで同様に解像度が仮に 1000 x 500 だったら、という条件で考えみると……
float minValue = min(1000.0, 500.0); // → 500.0
vec2 p = vec2(
(gl_FragCoord.x * 2.0 - 1000.0) / minValue, // → -2.0 ~ 2.0
(gl_FragCoord.y * 2.0 - 500.0) / minValue // → -1.0 ~ 1.0
);
こんな感じの計算をしているわけですね。
こうなると、変数 p の X 要素は、1.0 よりも計算結果のとり得る範囲が広くなってしまうことになりますが…… 実際に twigl.app 上でどんな感じになるのかやってみましょう。
precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;
void main(){
float minValue = min(resolution.x, resolution.y);
vec2 p = vec2(
(gl_FragCoord.x * 2.0 - resolution.x) / minValue,
(gl_FragCoord.y * 2.0 - resolution.y) / minValue
);
gl_FragColor = vec4(p.x, p.y, 0.0, 1.0);
}

パターン2のときと、パターン3では、どのように状態が変わったのかわかるでしょうか?
左下に黒の領域がある点は共通していますが、赤のグラデーションが「画面端に到達するよりも早い段階で完全な赤になっている」というのがパターン2との違いです。

GLSL では、負の領域や 1.0 よりも大きな数値はクランプ(丸め)が行われるため、正規化された座標が 1.0 よりも大きな箇所では、一様に 1.0 と同様の色が出力されている感じです。
なぜ min を使った正規化を行うのか
パターン3のような min 関数を使った正規化は、最初はちょっとその意図がわかりにくいかもしれません。
このような「短い辺の長さで正規化する」という場合、これは画面のアスペクト比の違いを吸収するためである場合が多いです。
たとえば、画面全体にグラフィックスを描画するような処理を行う際に、極端な話、スクリーンがめっちゃ横に長いとか、縦に長いという場合、普通に正規化した状態で描画を行ってしまうと、グラフィックスそのものが間延びしたような状態になってしまいます。
これを防ぐには、常に 短辺を基準として正規化を行ってやればよい わけで、 min 関数を用いた正規化がやっていることはまさにこれです。
twigl.app ではアニメーション GIF を出力する機能がありますが、正規化に min を使っているものと使っていないものを見比べてみると、特に「スクリーンのアスペクト比が正方形ではない場合」にその違いが顕著になります。
上段は、正規化をしていない。下段が正規化をしている場合。
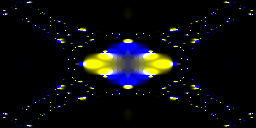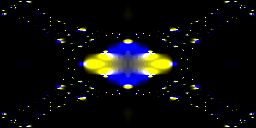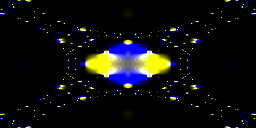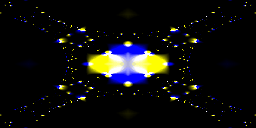

min 関数を使ってスクリーン座標の正規化を行っているコードを見かけたときは、アスペクト比にも考慮した座標の正規化をしているんじゃな! かっこいい! と考えてやればよいわけですね。
最後に
スクリーン座標の正規化という、特に初心者のうちはわかりそうでよくわからない事柄について説明してきました。
このような基本的なことって、意外と誰も教えてくれないというか…… 最初のころはちょっとわかりにくいものなんじゃないかなと思います。
なかなかド派手な絵が出てこなくてちょっと退屈に感じている人もいるかもしれませんが、こういった基本をおろそかにすると、結局どこかで遅かれ早かれつまづく場面が出てきます。まずは基本をしっかり積み重ねつつ、GLSL の独特なコードの書き方に慣れていきましょう。
次回は、正規化したスクリーン座標を利用してグラフィックスを描画する、具体的な例をいくつか提示できたらと思っています。
お楽しみに。



