【連載】#3 twigl.app で始める GLSL クリエイティブコーディング！ よく見る GLSL のビルトイン関数を知る

頻出するものから徐々に覚えていこう

twigl.app で始める GLSL クリエイティブコーディング、第三回となる今回のテーマは「よく使うビルトイン関数を知ろう」です。

GLSL に初めて挑戦するとき、大抵は、ちょっと変わったデータ型とか、スクリーン上の全てのピクセルでまったく同じ GLSL のコードが実行されるとか、そういうところで面食らってしまいます。しかし、そのあたりの原理が理解できてくると、次にぶち当たる壁として「で、どうしたらいいの？」というのが出てきます。

今回は GLSL のビルトイン関数にどのようなものが用意されているのか知りながら、それらの関数を使うことでどういった模様を描くことができるのか、そのパターンを把握していきましょう。

今回の記事ではグラフの描画に Desmos を使わせていただいています。

とても使いやすいツールなので、計算結果の可視化などに活用すると、学習の助けになると思います。

値の大小を色に脳内変換できるか

GLSL では出力される色を数値で考える場面が多いです。

というか、普段の生活で「色 ＝ 数値」という考え方をあまりしないというだけで、デジタルな世界では色は常に数値で表されるものですよね。HTML や CSS で色を扱うときも、基本的には「値の大小や、そのバランス」によって色を決めることになりますし、GLSL でも当然それは同じです。

ちょっと GLSL に特有かなと個人的に思うのは、数式（あるいは計算）の結果が色になる、という点だと思います。

色を塗るという行為がベタ塗り前提になっている CSS などの色指定とは異なり、GLSL では様々な計算の結果が色として出てくることになるので、最初はちょっとその感覚がね……難しく感じるのかなと思います。

とは言え、基本的に 難しい数学や数式をわざわざ持ち出さなくても 簡単な計算で十分に魅力的な画作りはできます。

要は、発想と工夫と手数、そして運です。

特に、偶然という名の「運」を味方につけるには、とにかく手数を増やしていくことが大事だと思います。ちょっとずつ、わかることからでいいので、自分なりにコードを書いてみましょう。

GLSL クリエイティブコーディングで頻出する関数たち

sin, cos

言わずと知れた、サインとコサインです。

まあこれがないと始まりませんわな。

サインやコサインというのは、あらゆる数学の分野で活躍するすごいやつだと思います。その利用シーンはあまりにも多岐にわたるため、こういうふうに使うべきだ～ みたいな特定の何かがあるわけではありません。

サインとコサインについてよくわからなかったとしても、使い方の例というか考え方のポイントとしては以下の点をまず意識するのがよいと思います。

• サインやコサインは引数に float を１つ取る
• 引数がどんなに大きくても小さくても戻り値は -1.0 ~ 1.0 の範囲になる
• time などの時間経過で増加する値を引数に与えると -1.0 ~ 1.0 の範囲を反復する

サインやコサインって、数学に苦手意識あったりすると頭の中でなんかよくわからないものとしてカテゴライズされてたりすると思うのですが（私は実際そうでしたね……）、使い方のコツとしてはとにかく上記に上げたような特性をよく理解しておくことです。

数学的なサイン・コサインの使い道は本当に無数にあるので、それらをひとつひとつ勉強していくのは実際大変です。ですからポイントを絞って「なんか反復させたいときに使う」とか、そういうところから覚えていくのも個人的にはアリかなと思います。（こんなことを書いちゃうと数学をきちんと勉強している人に怒られそうだけど）

連載の第一回のときも書きましたが、GLSL に限らず、勉強は楽しくやるべきです。難しくなってつらいだけになってしまうくらいなら、こういう緩い感じでいいからまず始めてみたほうがよほどいいでしょう。それは間違いないです。

では、具体的にいくつか例を出してみましょう。

サインやコサインは、だんだん増えるような値を引数に与えると、その結果は周期的に繰り返されます。

ですからたとえば以下のように出力する色を、時間の経過とサインなんかで脚色してやると……

precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;
void main(){
  // 時間の経過からサインの結果を得る
  float s = sin(time);
  // RGB にサインの結果を出力する
  gl_FragColor = vec4(vec3(s), 1.0);
}

twigl.app で DEMO を見る

どんな結果になったでしょうか。

たぶん、明るくなったり、暗くなったり、したんじゃないでしょうか。

サインの結果というのは、俗に言う「サイン波」の軌跡を描くので、これを色として出力すると「値がプラスになる時間帯は明るく」なるし、「値がマイナスになる時間帯は黒」になるわけですね。

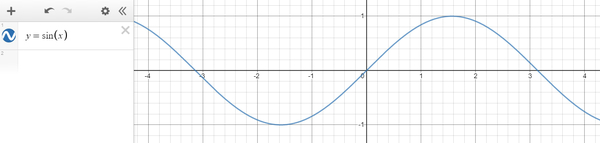
プログラミングの解説とかを読んでいるときに、こういう数学っぽい話（やグラフとか、数式とか）が出てくると急に難しそうな感じがするかもしれません。

ここでグラフをわざわざ表示している理由は「値がどのように遷移しているのかをわかりやすくするため」です。

先程掲載したコードでは sin(time) というように、サインの引数に時間の経過を与えていましたよね。

つまりこの場合、グラフの右方向を「時間の経過と共に引数の値が増え続けていく状態」と考えて、それに対してサインがどのような戻り値を返してきているのかということを考えると良いでしょう。

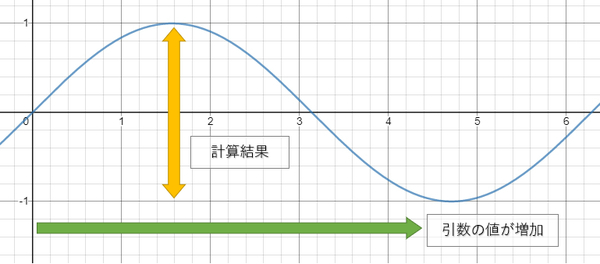
また、このとき、サインの計算結果がゼロ以下の値（負の数値）となった際に、描画結果が真っ黒になってしまうのはなんかオシャレじゃないな～ と思ったら、そんなときは次に紹介する abs を使ってみるのがよいでしょう。

abs

abs 関数は、日本語で言うなら「絶対値」というやつで、英語なら absolute value かな…… その最初の３文字を略した関数名ですね。

絶対値というのは、わかりやすくいうと「符号を無視して、マイナスの場合もプラスの場合も一様に扱う」という意味の値です。もっと砕けた言い方だと「マイナスもプラスとして扱う」と言ったほうがわかりやすいかもしれません。

先程、サインやコサインの戻り値は -1.0 ~ 1.0 の範囲で反復運動するというふうに言いましたが、場合によっては、負の数値になってほしくないんだよな～ っていうときがあったりします。

そんなときは abs 関数で絶対値を取ってしまいましょう。

たとえば、こんなふうに。

precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;
void main(){
  // 時間の経過からサインの結果を得る
  float s = sin(time);
  // サインの結果の絶対値を取る
  s = abs(s);
  // RGB にサインの結果を出力する
  gl_FragColor = vec4(vec3(s), 1.0);
}

twigl.app で DEMO を見る

さあどうでしょうか。

今度は、サインの結果が「負の領域に及ばなくなる」ことによって、結果的に色が明るい時間帯が増えたと思います。

これはサイン波が以下のような状態に変換されたということですね。

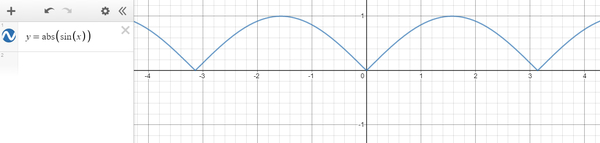
そして、この図で言うところの横軸は、やっぱり先程の説明と同様に単なる時間の経過なので……

たとえば時間の経過する速度を変化させてみたりすると、点滅する速度を速めたりすることもできます。（激しい点滅が苦手な人は十分気をつけてください）

precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;
void main(){
  // 時間の経過を速めてやると…… ※５倍速
  float s = sin(time * 5.0);
  s = abs(s);
  gl_FragColor = vec4(vec3(s), 1.0);
}

twigl.app で DEMO を見る

min, max, clamp

abs 関数を理解したことにより、マイナスの数値をプラスの領域へと閉じ込めることができるようになりましたが……

もっと柔軟に、様々な値に対して条件付きで制限したい場面も出てくるでしょう。

そういうときは min 関数や max 関数が役に立ちます。これらの関数は、その名前が示すとおり「最小値や最大値」を設定したい場合に利用できます。

たとえば、先程の abs 関数を使ったコードで「色が 1.0 で出力されると明るすぎるから、最大でも 0.5 までにしたい」と考えた場合は、次のようにすればよいですね。

precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;
void main(){
  float s = sin(time);
  // 小さい方を返す min を利用して最大値を 0.5 に制限
  s = min(abs(s), 0.5);
  gl_FragColor = vec4(vec3(s), 1.0);
}

twigl.app で DEMO を見る

min 関数は「与えられた引数のうち、小さいものを返す」という関数なので、最大値を設定するのに利用できます。逆に最小値を設定したいのであれば max 関数で「大きいものだけを返させる」ようにしてやればよいでしょう。

ちなみに、最小値と最大値を同時に設定できる clamp という関数もあります。

precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;
void main(){
  float s = sin(time);
  // 最小値と最大値を同時に設定する例
  s = clamp(abs(s), 0.25, 0.75);
  gl_FragColor = vec4(vec3(s), 1.0);
}

twigl.app で DEMO を見る

fract, floor

min や max とはちょっと違いますが、似たような使い方ができる関数に fract があります。

この関数は「小数点以下だけを返す」という性質があるので、結果的に clamp(t, 0.0, 1.0) と似たような感じの処理を実現できます。

任意の範囲を指定できるわけではなく、あくまでも「小数点以下を返す」だけですが、結構使える場面は多くあります。クリエイティブコーディングの用途では、時間を引数に与えて点滅（あるいはそのような動き）に使うことが多いかもしれない。

precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;
void main(){
  // 小数点以下を返させることで明暗をよりクッキリさせる
  float s = fract(time);
  gl_FragColor = vec4(vec3(s), 1.0);
}

twigl.app で DEMO を見る

結果だけを見ると、サイン波を色として出力したときとの違いがちょっとわかりにくいかもしれません。しかし、これは fract 関数を通した値がどのように遷移するのか、グラフにして見てみるとわかりやすいでしょう。

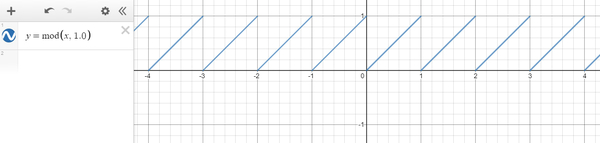
ご覧の通り、一定のところまで上昇した値が一気にゼロに戻るようなグラフになります。いわゆるノコギリ波の形ですね。

よりエッジの強い演出や動きには、サイン波によるなだらかな変化よりも、こういったクッキリとした変化のほうが適している場合もあるわけですね。

なお、この fract 関数と対になる意味を持つ floor 関数というのもあって、こちらは「整数部分だけを返す」という意味の関数になります。セットで覚えておくとよいかもしれません。

mod

GLSL クリエイティブコーディング界隈で結構よく見かける関数といえば mod 関数も外せません。

これはいわゆる「剰余（modulo）」を計算するためのもので、わかりやすく言えば「割った余り」だけを得たい場合に使います。第一引数に計算対象の値を入れて、第二引数に「割る数」を入れます。

float m = mod(t, 10.0); という感じ。これで、10 で割ったときの余りだけを抽出できるというイメージです。

どうしてこれがクリエイティブコーディング界隈でよく出てくるかというと、これを使うと手っ取り早く物量感を演出できる場面が結構あるからです。

precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;
void main(){
  // 100 で割って、その余りを取得（余りなので 0 ～ 99 の範囲になる）
  vec2 modulo = mod(gl_FragCoord.xy, 100.0);
  // 余りをさらに 100 で割って 0.0 ～ 1.0 未満に変換して出力
  gl_FragColor = vec4(modulo / 100.0, 1.0, 1.0);
}

twigl.app で DEMO を見る

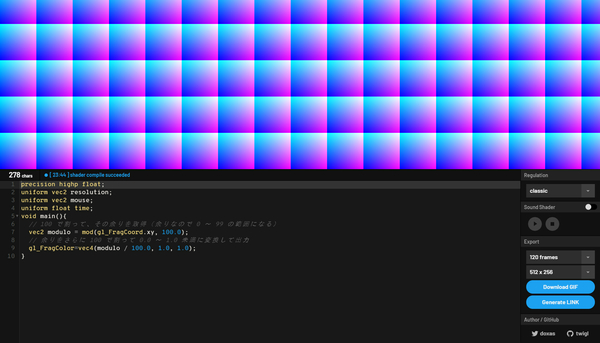
急に出力結果がカラフルになりましたね。

コメントに記載のあるとおりですが、特定の数を割った余りを利用するということは「一定の周期で繰り返すような座標系を作ることもできる」というわけです。上記の例で言えば gl_FragCoord.xy の値が 0.0 ~ 100.0 未満 になったことで、同じ模様が繰り返し現れるようになったわけです。

これは非常に応用の利くテクニックなので、覚えておくとよいと思います。

pow

pow 関数は、いわゆる「べき算」を行うための関数。

第一引数に対象となる値を与え、第二引数にその値を何乗するかを指定します。GLSL クリエイティブコーディングの文脈では、なだらかな線形の値の変化を pow 関数を使って歪ませるのに利用したりしますね。

どういうことか、言葉ではちょっとわかりにくいと思うのですが……

1.0 よりも小さな数値に対してべき算を行うと、乗ずる回数が多いほど急激な値の変化を得ることができます。

上段のグラフが２乗の場合、下の段が４乗の場合です。

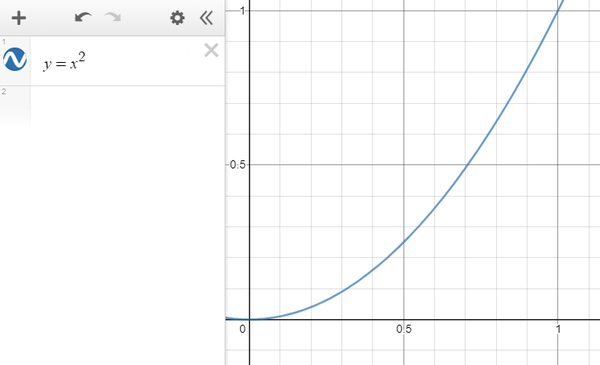
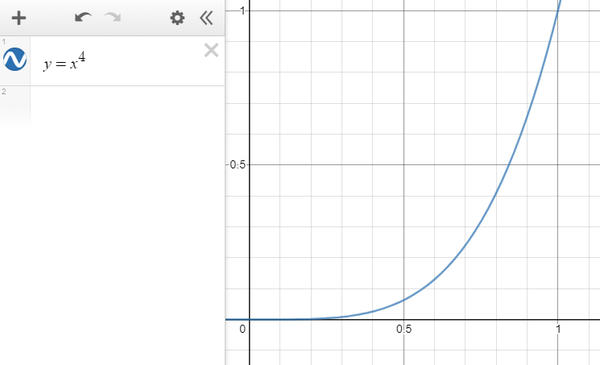
２乗の場合よりも、４乗の場合のほうがカーブが急になっているのがわかるでしょうか？

特に、光るような表現を行いたい場合なんかには、強力な光源を演出する意図で「大きい値の範囲を限定したい（減衰させたい）」といった場面があったりするので、このような演算により演出品質が向上することがあります。

光っているように見える範囲が広すぎる場合、なんかうっすらと靄が掛かったような印象になるというか…… 印象もぼやけてしまうんですよね。

その点、 pow などを使って減衰させた値で表現すると、光っているように見える明るい範囲が狭く限定されることによって、逆に強い光のような印象になったりします。（あくまでも利用例の一例なので、もちろん他にも使い道はいろいろあります）

precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;
void main(){
  // X 方向 200px ごとに正規化
  float moduloX = mod(gl_FragCoord.x, 200.0) / 200.0;
  // これを３乗した値を計算しておく
  float powX = pow(moduloX, 3.0);
  // 画面の上半分と下半分で出力結果を変える
  float dest = 0.0;
  if(gl_FragCoord.y / resolution.y > 0.5){
    dest = moduloX;
  }else{
    dest = powX;
  }
  gl_FragColor = vec4(vec3(dest), 1.0);
}

twigl.app で DEMO を見る

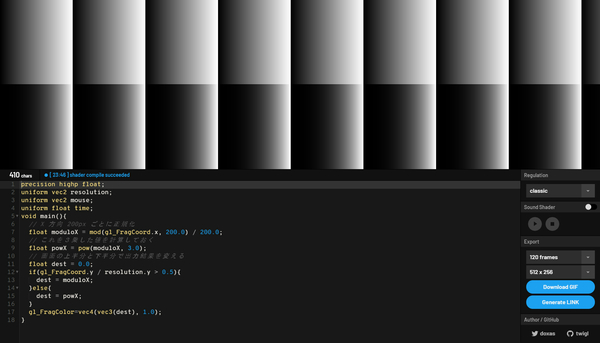
画面の上半分と、下半分とで、明るい領域の濃淡に違いがあるのがわかるでしょうか？

pow 関数を使ったことにより、値が減衰するように急激に小さくなることで、結果的に白い部分がより強調されたような感じになるわけですね。

step

step 関数はちょっと特殊な関数で「ある条件を満たした場合だけ 1.0 を返し、そうでない場合 0.0 を返す」という不思議な関数です。

その条件とは「第一引数が、第二引数より小さい」です。

こんな関数つかうことある！？ そう思いませんか……私は始めてこの関数の存在を知ったとき、恥ずかしながらそんなふうに思いました。

でもこの step 関数、実は if による条件分岐の代わりに使える場合があるのです。実際に、どんな感じで書くか、先程の pow 関数のときのコードで使っていた if 文を step 関数を使ったバージョンに置き換えてみましょう。

precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;
void main(){
  float moduloX = mod(gl_FragCoord.x, 200.0) / 200.0;
  float powX = pow(moduloX, 3.0);
  // step 関数の戻り値は 0.0 OR 1.0
  float st = step(0.5, gl_FragCoord.y / resolution.y);
  // 座標により dest の結果が変わる
  float dest = st * moduloX + (1.0 - st) * powX;
  gl_FragColor = vec4(vec3(dest), 1.0);
}

twigl.app で DEMO を見る

さて…… どうでしょう……

ちょっと頭の体操的な内容ですが、実際に起こっていることは実にシンプルな単純計算です。

gl_FragCoord.y / resolution.y の結果が 0.5 より大きくなるときと、そうでないとき。両方のケースを考えてみると、どうしてこれで if 文を書いていないにもかかわらず、条件分岐ができているのか、わかるんじゃないでしょうか。

#define マクロ

今回紹介してきたビルトイン関数たちとはちょっと違いますが、最後に GLSL でも利用できるマクロについて簡単に説明しておきましょう。

#define という記述を使うと、マクロを定義することができます。

単純に「コードの文字列を置き換えて実行する」というちょっとテクニカルなことを実現できます。これは実際に、その使い方を見たほうが早いかも知れません。

precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;

#define A abs(sin(time))

void main(){
  gl_FragColor = vec4(vec3(A), 1.0);
}

twigl.app で DEMO を見る

上記の例では A というアルファベット一文字をマクロとして登録していて、コード内に A が出てきた部分に abs(sin(time)) が置換されたあと、それが最終的なコードとして実行されます。

基本的には「何度も繰り返し出てくるような処理を関数的に使っている」ということなんですが……

たとえば、#define マクロを活用すると次のようなこともできます。

precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;

#define A(arg) abs(sin(time * arg))

void main(){
  gl_FragColor = vec4(A(2.0), A(3.0), A(4.0), 1.0);
}

twigl.app で DEMO を見る

まるでマクロって関数みたいですよね。

ただ、マクロは関数と似たようなことができますが、関数とはまったく違います。GLSL で関数を定義する場合、引数のデータ型などをしっかり指定してやらないといけないので、先程の A(arg) マクロと同じことを関数で書こうとすると……

precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;

float A(float arg){
  return abs(sin(time * arg));
}

void main(){
  gl_FragColor = vec4(A(2.0), A(3.0), A(4.0), 1.0);
}

こんな感じになります。

関数で書く場合にはどうしても「型が固定される書き方」になってしまうわけです。ところが #define マクロっていうのは「単純な文字列置換」なので、データ型に対する汎用性を持たせることができたり、あるいは関数では代替不可能なものを置き換えたりといったことができます。

場合によっては、ほとんど無意味な置換とかもできます。

たとえばこんな感じの。

precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;

#define f float
#define t time

// マクロが定義されているので float を f と書ける
f A(f arg){
  // マクロが定義されているので time を t と書ける
  return abs(sin(t * arg));
}

void main(){
  gl_FragColor = vec4(A(2.0), A(3.0), A(4.0), 1.0);
}

ここ最近 #つぶやきGLSL タグで投稿されている「極端に minify された GLSL」には、結構 #define が使われているものが多いですが、単純な文字列置換だからこそのメリットを最大限に活かして、長いキーワードやロジックをアルファベット一文字で短く記述できるようにしているわけですね。

初心者のうちからあまり意識するとぐちゃぐちゃになるので、マクロなんかは GLSL が自然に記述できるようになってから、使うようにすることを個人的にはおすすめします。

まとめ

さて、今回は GLSL で、特にクリエイティブコーディングの文脈で頻出するビルトイン関数を使って、いくつか表現の例を示してきました。

GLSL では短いコードで様々なことができますが、それらの多くは「小技と小技の足し算、あるいは掛け算」で実現されていることも多いです。たとえば、今回登場した mod や fract などを組み合わせると、簡単に座標系が繰り返されるような状態を作ることができますし sin や cos を用いれば、反復運動や明滅が表現できます。

こういった小さなテクニックの組み合わせから、記述者本人も想像していなかったような、思わぬ描画結果や表現が生まれるのです。だからこそ、しっかりと基本を押さえておくのが大切だと私は思います。

ぜひ自分なりの表現を探してみてください。

次回は、ベクトルを使って画作りを行う基本を扱う予定です。

お楽しみに。

リンク：

Desmos | Beautiful, Free Math

twigl.app