
【連載】#4 twigl.app で始める GLSL クリエイティブコーディング! ベクトルを理解し仲良くなろう
ベクトル!? なにそれおいしいの
twigl.app で始める GLSL クリエイティブコーディング、第四回のテーマは「ベクトルと仲良くなろう」です。
ベクトルって、GLSL に限らず、3DCG の世界ではとってもポピュラーな存在ですが、一方で実生活で(一般的には)ほとんど会話に出てこない概念ですし、私のように学生時代の記憶が諸事情により忘却の彼方という方々にとっては、いまいちよくわからない存在なんじゃないでしょうか。
「ベクトル」や「行列」という言葉が出てくるだけで難しそうと感じてしまう人も多いかもしれませんが、なんとか少しでも、それらの概念が身近に感じられるように解説してみたいと思います。
数学的解釈と GLSL 的解釈
最初に言い訳をしちゃうのですが、数学的に正しくベクトルを説明することは、正直私にとってもかなり難しいことなので……
今回の記事ではあくまでも「GLSL クリエイティブコーディングの文脈」という前提で、表現につながるようなベクトルの活用方法を紹介していこうと思います。
クリエイティブコーディング的な実装を行う場合に限らず、GLSL や一般にシェーダーと呼ばれているプラットフォーム上では、あらゆる利用シーンでベクトルや行列がたくさん出てきます。ですから GLSL の場合も、コード記述の利便性の観点からだろうと思いますが、連載の第一回で解説したような vec2 とか vec3, vec4 といった「ベクトルを扱うデータ型」が初めから用意されています。JavaScript にもあったらいいのに……
数学的な見方をすると、ベクトルには、ベクトル同士の加算や減算の他に「内積」や「外積」などがありますが、ベクトル同士の「除算」は存在しません。割り算はできないということになってるわけです。(と、私は理解してます)
でも、これ実は、GLSL だとコード上はそういう書き方もできます。
vec3 v = vec3(8.0) / vec3(4.0);
ベクトル同士の割り算はできないはずなのに、こういう書き方はできますし、エラーにはなりません。上記の変数 v の中には vec3(2.0, 2.0, 2.0) みたいな感じで値が入っています。
つまり、実際には以下のようなことが起こってるんですね。
vec3 v = vec3(
8.0 / 4.0, // x 同士で除算
8.0 / 4.0, // y 同士で除算
8.0 / 4.0 // z 同士で除算
);
それぞれの要素同士で、四則演算を行ってる感じです。このあたりは、本来の数学におけるベクトルの特性とは、ちょっと違った GLSL 特有の挙動をするわけですね。
ちなみに、以下のようにベクトルとスカラー(ベクトルではない単一の実数)を四則演算することもできます。
vec3 v = vec3(8.0) / 4.0;
この場合も、やはり変数 v には vec3(2.0) 相当の結果が入ります。
つまり GLSL の世界のベクトルは、同じ要素数同士のベクトルであれば各要素ごとに四則演算が行われます。またいかなる要素数のベクトルでもスカラーとの四則演算が行なえますので、覚えておくとよいでしょう。
ベクトル定義時の数値の指定
GLSL は数値の扱いが非常に厳密な言語です。整数と、浮動小数点の数値は、データ型が異なるためそのままでは両者を同時に計算することができません。つまり
1 + 1.0みたいな書き方はエラーになります。(整数と浮動小数点の値を加算しようとしているからエラー)そして GLSL のベクトルって、各要素は
floatとして扱われます。その前提に立って普通に考えると
vec3(0)のように「引数に整数を指定する」という行為はうまくいかないような感じがしてしまいます。しかし、実際にはこれは普通にうまくいきます。なぜそのようなことが起こるのかというと、実はこれめっちゃ簡単な話でして、
vec2()のようにコンストラクタのような感じでベクトルを定義するときの「引数の指定は整数でもいいよ!」ってことに仕様上なってるのですね。ですから #つぶやきGLSL のような極端にコードを短く記述する必要性がある場面では、わざわざvec2(0.0)のように書かなくてもvec2(0)で2文字削減できます。やったね!
ベクトルには向きと長さが備わっている
ベクトルの説明としてよくある一文に「ベクトルは向きと大きさを持った量である」っていうのがあると思うのですが、この日本語、私は最初「意味わからんすぎて逆にすごいな!」と思いました。(たぶん30歳くらいのとき)
ベクトルについて理解が深まってくると、この意味不明な日本語が「なるほど、たしかにそうとしか言い表せないな! ハッハッハ~」という感じになってきます。不思議ですね……
ベクトルには、先述のとおり「向き」という概念と同時に「大きさ(または長さ)」という概念が備わっています。
これ、文章で聞くとよくわからないかもしれないのですが、ベクトルを矢印で表して並べてみると、意味がちょっとわかったような気持ちになれるかもしれません。
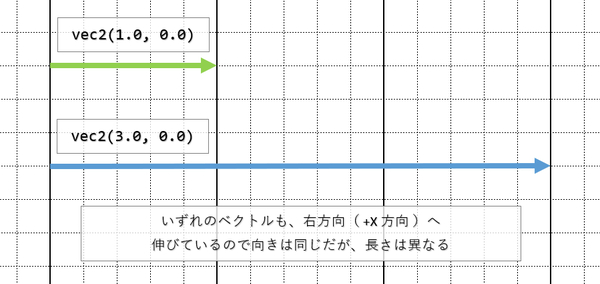
ベクトルというのは、数値の組み合わせを使うことで、その数値同士の比率によって向きが表現できます。たとえば vec2(1.0, 0.0) だとしたら、X 方向にまっすぐ向いているな! ということはたぶんすぐに分かると思います。同じように vec2(3.0, 0.0) だとしても、やっぱり X 方向にまっすぐ向いているな!? ということはわかりますよね。でも、これを両方とも矢印で表現してみると、あきらかに両者の大きさ(長さ)が異なっています。
このようにベクトルには、向きと大きさという概念が同時に含まれているのですね。
またベクトルには、しばしば「単位化(または正規化)」と呼ばれる変換を適用することがあります。
これは ベクトルの大きさを1ぴったりに変換する 行為を表しており、大抵のベクトルは基本的に単位化して大きさを強制的に1ぴったりにすることができます。(ゼロベクトルとか一部例外があります)
どうして単位化を行うのかと言うと、大きさが1だと単純に都合が良いからです。たとえば「ベクトルが指し示す方向に歩くマン」がいたとしますね。このベクトルが指し示す方向に歩くマンは、自分が与えられたベクトルを単位化する機能を持ってないものとします。
すると、長さが1のベクトルを与えられた歩くマンと、長さが3のベクトルを与えられた歩くマンでは、その歩行速度に単純に差が生まれます。
歩くマンの歩幅 = ベクトル * 1歩;
こうなるからです。ベクトルの長さが長ければ長いほど、歩幅が大きくなるわけです。
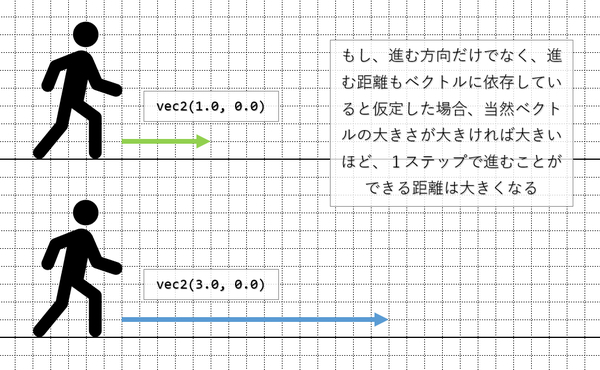
ここでは人間に例えましたが、仮にこれがアクションゲームのキャラクターの移動や、あるいは敵の放った銃弾とかに置き換えて考えてみると、ベクトルの長さが一定ではないことによって様々なトラブルが発生しそうな予感がしてくるのではないでしょうか。
ここではゲーム的な視点に例えましたが、GLSL や 3DCG、あるいは数学の世界でも、ベクトルの長さを一定にしたい場面というのはかなりたくさん登場します。そこで、GLSL の場合はビルトインの関数を使って簡単にこれが実現できるようになっています。
vec3 v = vec3(3.0, 2.0, 1.0);
vec3 w = normalize(v); // 単位化!
このように normalize 関数を使うことで、ベクトルを単位化することができます。
ちょっと話が煩雑になったのでまとめておくと、ベクトルとは 向きと大きさを両方同時に表すことができる ものであり、また 向きだけに注目したい場合は単位化することで大きさを一定に揃える ことができます。
GLSL の場合はベクトルの単位化には normalize 関数を利用することができ、ベクトルの要素数に関係なく、この関数を通すだけでベクトルは常に大きさ1の単位ベクトルに変換することができます。今回の記事では解説しませんが、将来的にレイマーチングなどに挑戦したい場合にはこのあたりの知識が欠かせないものになってきますので、余裕があったら覚えておくとよいでしょう。
ベクトルと座標は別物
ベクトルは、向きと大きさを持った量だということが、なんとなくイメージできるようになったでしょうか。
さてここでめっちゃ大事な話をするのですが、ベクトルと、座標は、いずれも vec2(1.0, 0.0) みたいな感じで表現できます。 vec2(1.0, 0.0) をベクトルだとして見た場合は、X 軸に水平な右向きのベクトルってことになるのですが、これを座標として見てしまうと X 方向に 1.0 移動した位置、ということになってしまいます。
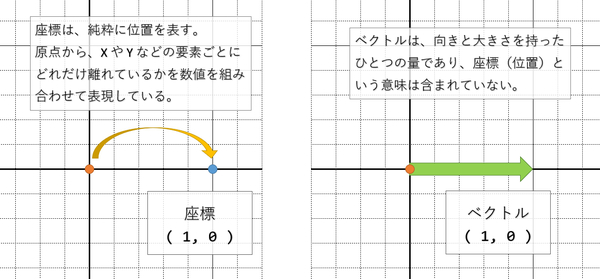
これは私の経験則なので、もしかしたら全然そんなことはない! という反対意見もあるかもしれませんが…… GLSL やベクトルの扱いに慣れているひと同士のやりとりでは、このあたりの「それはベクトルなんですか、それとも座標なんですか」という前提条件が 言わずとも暗黙でニュアンスが通じてしまっていて普通に会話が成立してしまう 場合が多い気がします。
ですからそもそも数学的な予備知識が無かったり、そういった会話を聞き慣れていなかったりする場合、はたから見ていてもその人たちが何について話しているのかがよくわからなかったりするんですよね。
ですから最初のうちは特に、今自分が扱おうとしているのが「ベクトル」なのかそれとも単に「座標」なのか、より意識してコードを書くようにするのがおすすめです。
本稿では、以降の解説でできるだけベクトルなのか座標なのかをしっかり明記するようにしますが、どちらも「コード上の表現はまったく同じ」なので、頭が混乱しないように注意しましょう。
まずは長さを測ってみよう
ではそろそろ、具体的に GLSL のコードを見ながら考えていきましょう。
ベクトルをクリエイティブコーディングに活かす、という意味で言うと、もっとも手軽なテクニックとしては「ベクトルの長さを測ってそれを表現に利用する」ことじゃないかなと思います。
たとえば次のようなコードはどうでしょうか。
precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;
void main(){
// スクリーン全体を -1.0 ~ 1.0 に正規化
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / resolution;
// 正規化した位置ベクトルの長さを測る
float l = length(p);
// 測った長さをそのまま RGB に色として出力
gl_FragColor = vec4(vec3(l), 1.0);
}
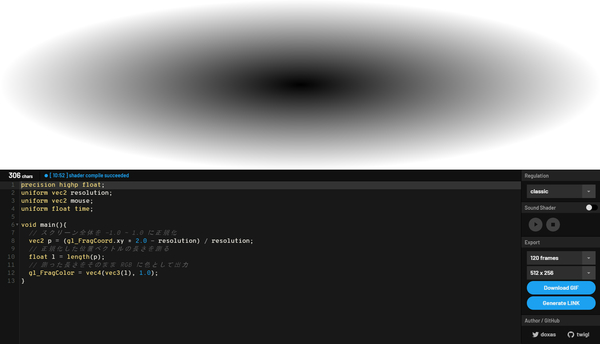
さて、ここではコメントをよくよく見てみることが肝心です。main 関数のなかにあるコメントに「正規化した位置ベクトル」と書かれている箇所がありますね。
このコメントにある通り、ここでは「位置ベクトル」つまり「座標をベクトルとみなして」その長さを測っています。
ここはちょっとわかりにくいところだと思いますので、しっかり説明します。
連載の第二回で触れたように、GLSL クリエイティブコーディングでは一般に「座標を正規化して原点を画面の中心に持ってくる」ということをよくやります。GLSL の本来の原点は左下隅の位置ですが、これを画面のど真ん中に持ってくるような変換を行うわけです。
ここでは例として、とあるピクセルだけに注目して、仮想的に計算を行ってみましょう。
たとえば、スクリーン全体が幅 1000px、高さ 500px だとします。さらにこのとき、注目するピクセルが 700.0, 400.0 の位置だと仮定してみましょう。
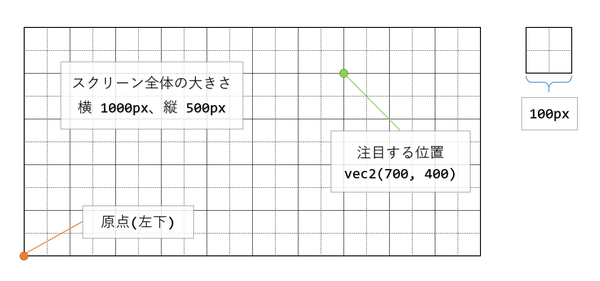
vec2(700.0, 400.0) というのは、「画面左下隅が原点で、かつ正規化していないときの座標」ですよね。言い換えると gl_FragCoord.xy そのままの値、と言ってもいいかもしれません。
これを uniform 変数 resolution も活用しながら -1.0 ~ 1.0 の範囲になるように正規化すると、次のようになります。
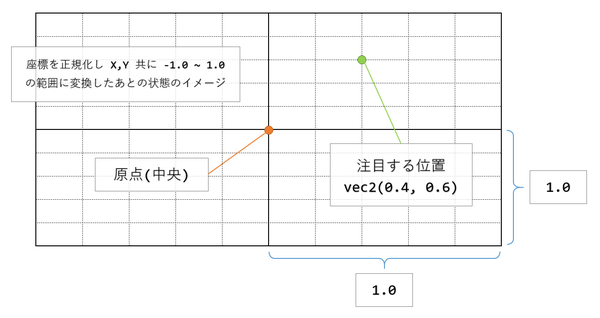
この状態だと、もともと vec2(700.0, 400.0) だった座標が vec2(0.4, 0.6) になっている形です。
そしてここで出てきた vec2(0.4, 0.6) っていうのはあくまでも「座標」です。向きと大きさを持った量であるベクトルではなく、ただ単に位置を指し示しているだけなんですね。
ですが、GLSL のクリエイティブコーディング的観点では、ここでこの「座標」をそのままベクトルのようにみなしてしまい length 関数を使って長さを測ったりすることがよくあります。これは図解すると、次のようなことを行っているのに等しいです。
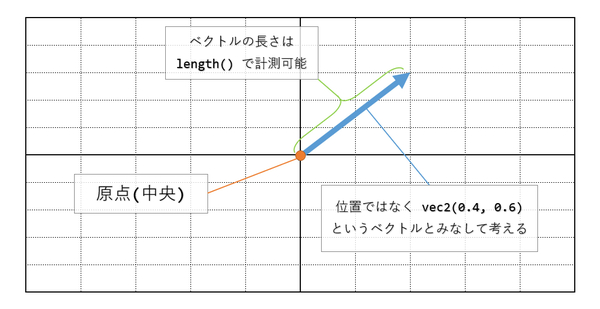
本来は座標であるはずの XY の数値をベクトルとみなして長さを測り、その結果を色としてプロットしています。
ですから、最終的な出力結果を見ると、画面の中央に近いピクセルほど「ベクトルとみなして測った長さが短い(つまり結果が小さな値である)」ために暗くなり、画面の端に近づくほどに「ベクトルとみなした場合に長い(つまり結果が大きな値である)」から白っぽくなっていくわけですね。
サイン・コサインや abs と組み合わせてみる
先程の例のように、座標をベクトルとして距離を測り、その結果を使ってなにかしらの表現を行うというのは慣れてくればそんなに難しくはありません。
たとえば、第三回で登場したサインやコサイン、あるいは絶対値を取る abs 関数などと組み合わせるだけでも結構いろんなことができますね。
いくつか例を見てみましょう。
まずはサインとの組み合わせの例です。
precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;
void main(){
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / resolution;
float l = length(p);
// 測った長さを sin 関数の引数に指定する
gl_FragColor = vec4(vec3(sin(l * 50.0)), 1.0);
}
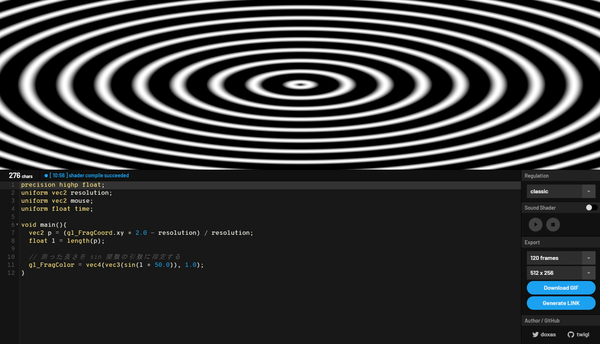
座標を正規化してベクトルとしてみなした場合、画面の中央から遠ざかるほど値が大きくなるような結果を得られます。ですから、それをそのままサインの引数に与えれば、まるで円形に広がる波紋のような模様を描くことができます。(そのままだと反復回数が少なすぎるので、ここでは50倍にスケールしています)
サイン波は、値が規則正しく上下するので、明るい → 暗いを繰り返す様子が波紋のように浮かび上がるという寸法です。
さらに abs 関数と組み合わせてみたり……
precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;
void main(){
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / resolution;
float l = length(p);
// sin の結果は -1.0 ~ 1.0 を反復するので、絶対値を取る
gl_FragColor = vec4(vec3(abs(sin(l * 50.0))), 1.0);
}
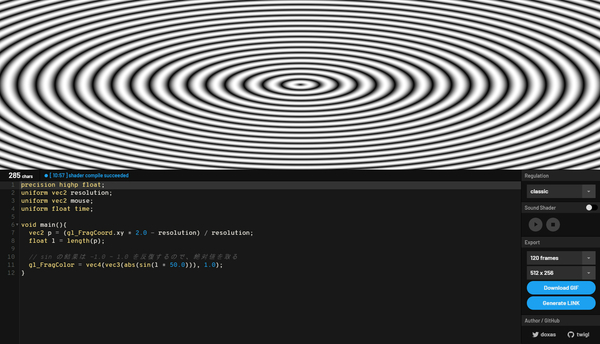
あるいは RGB のそれぞれに対して出力される色を……
ほんの少しずつサインに掛かるスケールを変えることでずらしてみたりとか。
precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;
void main(){
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / resolution;
float l = length(p);
// RGB で少しずつ周期のスケールをずらしてみる
vec3 color = vec3(
sin(l * 50.0),
sin(l * 47.5),
sin(l * 45.0)
);
gl_FragColor = vec4(abs(color), 1.0);
}

さらに、ベクトルの長さを測った結果(原点から遠いほど値が大きくなる)を、上手にクランプしてから全体に乗じてあげれば、ヴィネットのような効果を得ることもできます。
precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;
void main(){
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / resolution;
float l = length(p);
vec3 color = vec3(
sin(l * 50.0),
sin(l * 47.5),
sin(l * 45.0)
);
// 原点からの距離を 1.0 から引いた値を計算しておき色に乗算
float vignette = clamp(1.0 - l, 0.0, 1.0);
gl_FragColor = vec4(abs(color) * vignette, 1.0);
}
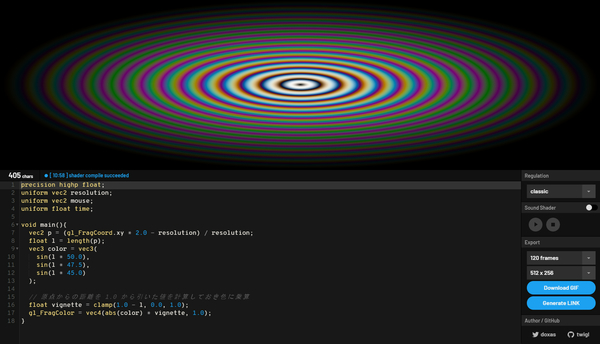
このような感じで、ベクトルの長さを測ることひとつとっても、その表現の方法は様々考えられます。
また、一番最後の例などが顕著かなと思うのですが、これらの表現方法っていうのは「複数同時に組み合わせることで様々な可能性が広がる」ものなのですね。
だからこそ、小さなアイデア、小さな引き出しをできるだけ多く身につけておき、それらを即座に組み合わせられるようになっておくことが表現の幅を広げるコツだと思います。
時間の経過とも組み合わせてみよう
さらに表現の幅を広げるためには、時間の経過を上手に活用することも覚えておきたいところです。
たとえば先程までの例に、時間の経過を加えてやるとしたら次のような感じでしょうか……
precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;
void main(){
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / resolution;
float l = length(p);
vec3 color = vec3(
// サインの計算結果が時間の影響を受けるようにする
sin(l * 50.0 - time),
sin(l * 47.5 - time),
sin(l * 45.0 - time)
);
float vignette = clamp(1.0 - l, 0.0, 1.0);
gl_FragColor = vec4(abs(color) * vignette, 1.0);
}
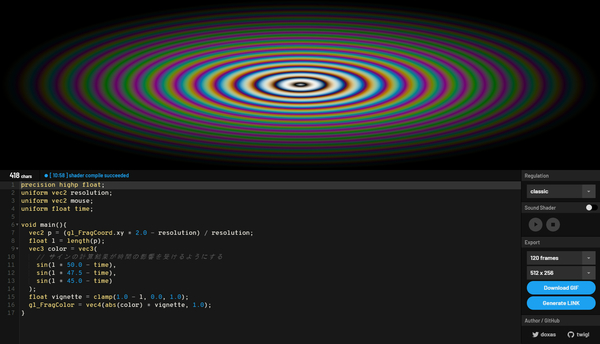
静止画のスクリーンショットでは流石にちょっとわかりにくいと思いますが、実際に動いている様子を見ると、かなり怪しくうごめいている様子が確認できると思います。
変化したのは「サインの引数に時間の経過が影響するようにした」という点だけなのですが、印象はかなり変わったんじゃないでしょうか。
これをさらに発展させて、RGB ごとに時間の経過速度が違ったとしたら、どうなるでしょう。
precision highp float;
uniform vec2 resolution;
uniform vec2 mouse;
uniform float time;
void main(){
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / resolution;
float l = length(p);
vec3 color = vec3(
// サインの計算結果が時間の影響を受けるようにする
sin(l * 50.0 - time * 2.0),
sin(l * 47.5 - time * 4.0),
sin(l * 45.0 - time * 6.0)
);
float vignette = clamp(1.0 - l, 0.0, 1.0);
gl_FragColor = vec4(abs(color) * vignette, 1.0);
}
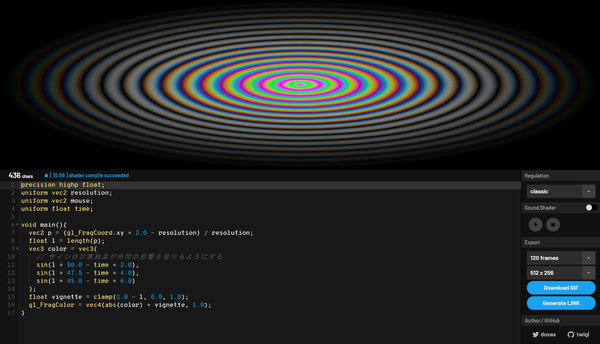
また一味変わった表現になったのではないでしょうか。
規則正しく上下するサイン波の特性と、位置ベクトルの原点からの距離、そして時間の経過などを組み合わせてやることで、このような画作りができました。
1つ1つのパーツは、どれもシンプルな計算ばかりだと思います。
最初は一気に全容を把握するのがちょっとむずかしいかもしれませんけれども、少しずつ、慣れていきましょう。
まとめ
今回はベクトルをテーマのひとつとして、様々な側面から考え方や表現につなげる方法を解説してきました。
以前、サインやコサインを紹介したときにも同じようなことを書いたのですが、ベクトルというのはあまりに多彩な活用方法がある概念なので、ここで示したのはあくまでも一例にしかすぎません。
また冒頭でも書いたように、GLSL のクリエイティブコーディングを行うという文脈で考えるベクトルは、GLSL 特有の考え方や捉え方が必要となることもあるので、やっぱり慣れも必要かなと思います。
日常生活でベクトルを使ってなにかをするということは、まあ普通に考えればほとんど無いはずです。実際、私も普段の生活の中で実際にベクトルを使って計算するっていうことは(プログラムを書くこと以外では)ほとんどありません。だからこそ 意識して使っていく、コードを書いていく ということをしないと、いつまで経っても知識が身につきません。
最初はちょっと難しく感じるかも知れないですが、少しずつでもいいのでぜひチャレンジしてみてください。



